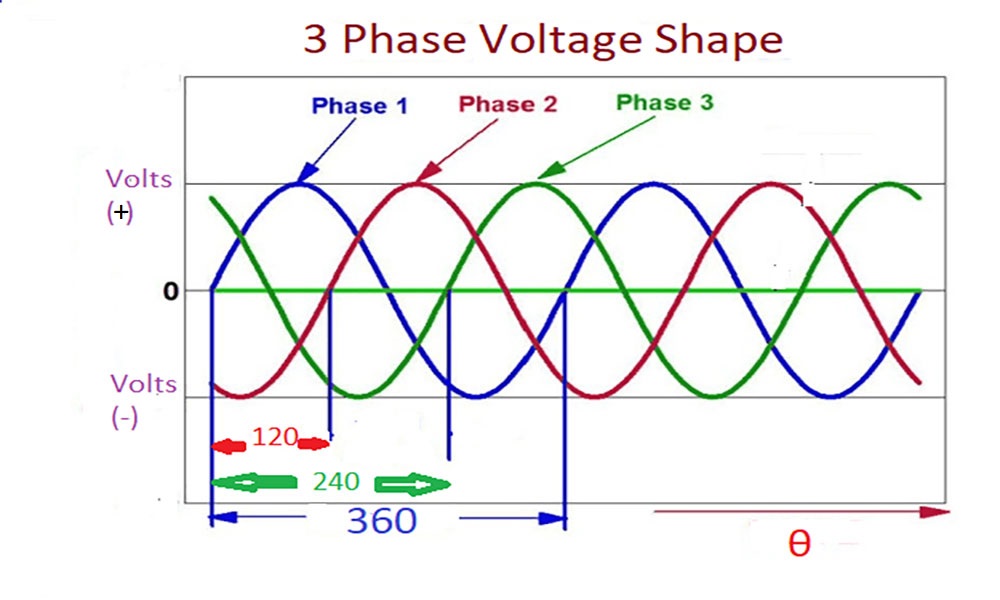
Description :
Since the 3 phases ( both for voltage & current waveform ) are 120 degrees out of phase from each other, therefore 3 phase power is constant.
We can find it from mathematical proof that three-phase instantaneous power
P = 3* Vp*Ip* cos φ, constant all time
where Vp = phase voltage, Ip = phase current, φ =phase diff. between current & voltage
Lets instantaneous voltage , v1= Vpeak * sin θ , v2= Vpeak *sin (θ-120) , V3= Vpeak *sin (θ-240)
AND instantaneous current, i1= Ipeak * sin (θ-φ) , i2= Ipeak * sin (θ-120-φ) ,i3= Ipeak * sin (θ-240-φ)
So, total instantaneous powers , P= v1 *i1 +v2 *i2+v3 *i3 =Vpeak * sinθ *Ipeak * sin (θ-φ) +Vpeak*sin (θ-120)*Ipeak * sin (θ-120-φ) +Vpeak*sin (θ-240)*Ipeak * sin (θ-240-φ)
Solving the equation, we get P = (3/2)*Vpeak*Ipeak*cos (φ).
But Vpeak = √ 2 Vp & Ipeak = √ 2 Ip
Therefore, Total Instantaneous Power, P = 3 *Vp*Ip*cos (φ)